How is spintronics a physical counterpart of electronics?

How is spintronics a physical counterpart of electronics? The absolute best way to learn is to play through Spintronics Act One and Act Two. It will give you a broad understanding, while the topics discussed here are specific and geared toward people who are already familiar with electronics. Have a question not covered here? Post a question on the spintronics community forum or email us at [email protected].

Spintronic circuits and circuit diagrams

Where is ground?

Limitations of spintronics

Advantages of spintronics

Spintronic and electronic units

We'll start by looking at how spintronic circuits relate to the circuit diagrams you're used to seeing. The key is to remember that all circuits, no matter how complicated, are just loops. Here's the basic spintronic circuit of a battery and a resistor (A), along with two equivalent circuit diagrams (B and C):

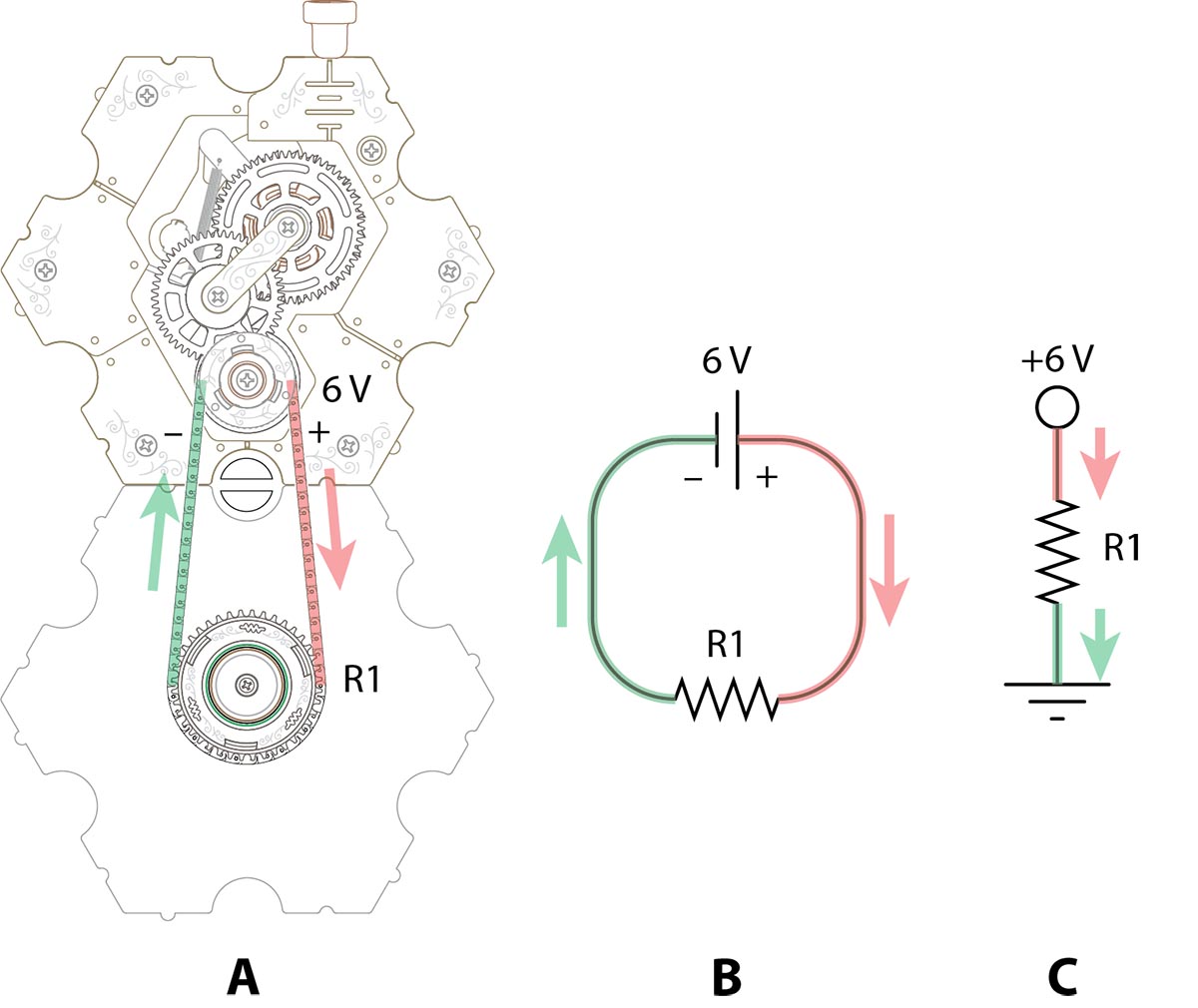
Three equivalent circuits. Red chains (wires) are at +6 V, green chains are at ground.

In spintronic circuits, a battery pushes chain into the circuit on one side (red paths) and the same amount of chain returns to the battery on the other side (green paths). In the picture above, the green paths would conventionally be called "ground." (But just like in electronics, the point you choose to call ground is arbitrary.)

That's pretty straightforward, but what about a little more complicated circuit? The circuit below has a junction that splits the current two ways. A1 shows the current leaving the spintronic battery and splitting along two paths at the junction (B1 and C1 show equivalent circuit diagrams.)

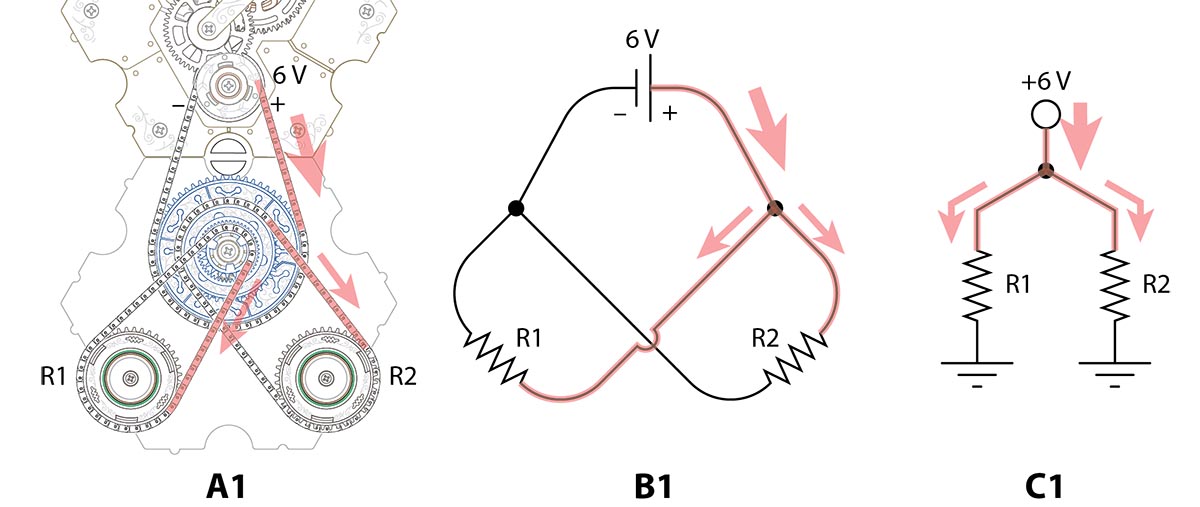
Before current can return to the battery, the two paths must join back together. In spintronic circuits, the paths rejoin at the same junction that split them.

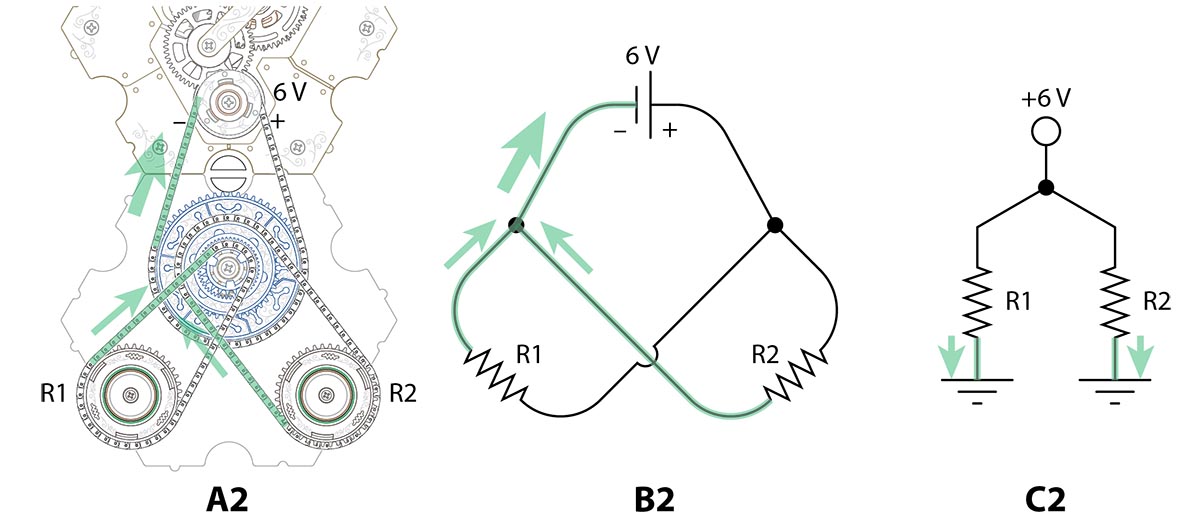
Even in much more complicated circuits like this next one, it's always the same: the current leaves the battery, splits up and does a bunch of interesting things, and then rejoins before returning to the battery.

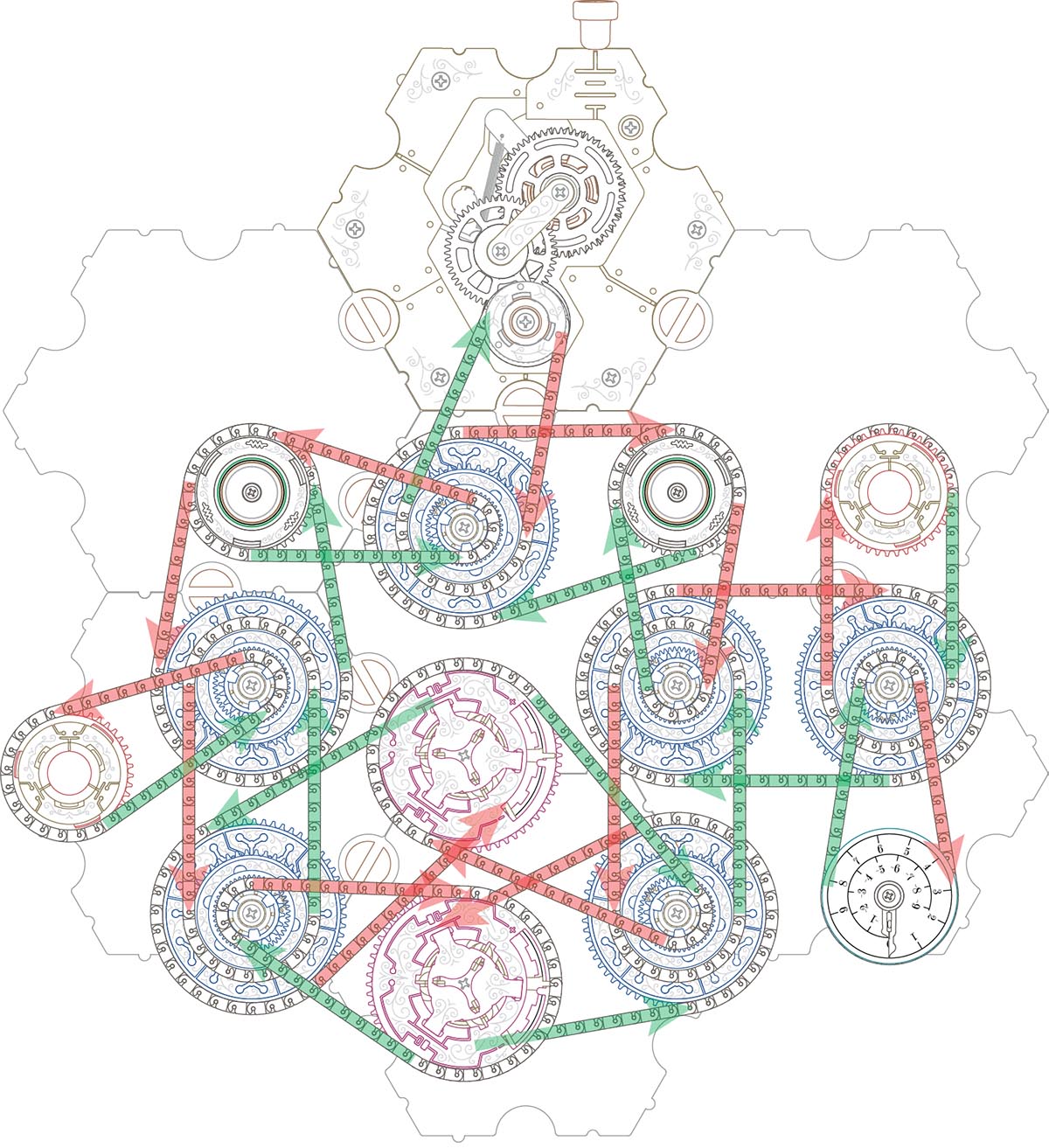
Even complicated circuits start as a single path that splits into many paths (red paths), but they all rejoin back into a single path before they return to the battery (green paths).

Like electronics, it's wherever you want it to be. But the most practical place for it to be is anywhere there is zero force (i.e., voltage) on the chain.

In theory, you could build the spintronic equivalent of any electronic circuit, though in the current implementation of spintronics, there are some important limitations. Spoiler: spintronics won't replace the electronics that power your home anytime soon.

One major limitation comes from stray inductance and capacitance, which limit you from building high frequency circuits. But perhaps the biggest limitation is that there is a limited dynamic range. For example, while you can find electronic resistors with values from microohms (10^-6) to teraohms (10¹²), spintronic resistors are currently only available in the range of 50 ohms to 5,000 ohms.

Then, of course, there's the size of the components. Spintronic transistors are about half the size of the first vacuum tubes from the early 1900's, but about a billion times larger than the transistors in your computer.

Despite these limitations, you'll be surprised at how much you can do. You can take most circuits and build equivalent, working circuits in spintronic form.

Obviously the biggest advantage of spintronics is that it makes electronics tangible. There's nothing else like it. But there are actually some useful things that can be done with spintronics that aren't nearly as easy with electronics. For example, you can generate a negative voltage simply by placing a part on the outside of a chain loop. A positive voltage becomes negative voltage just like that!

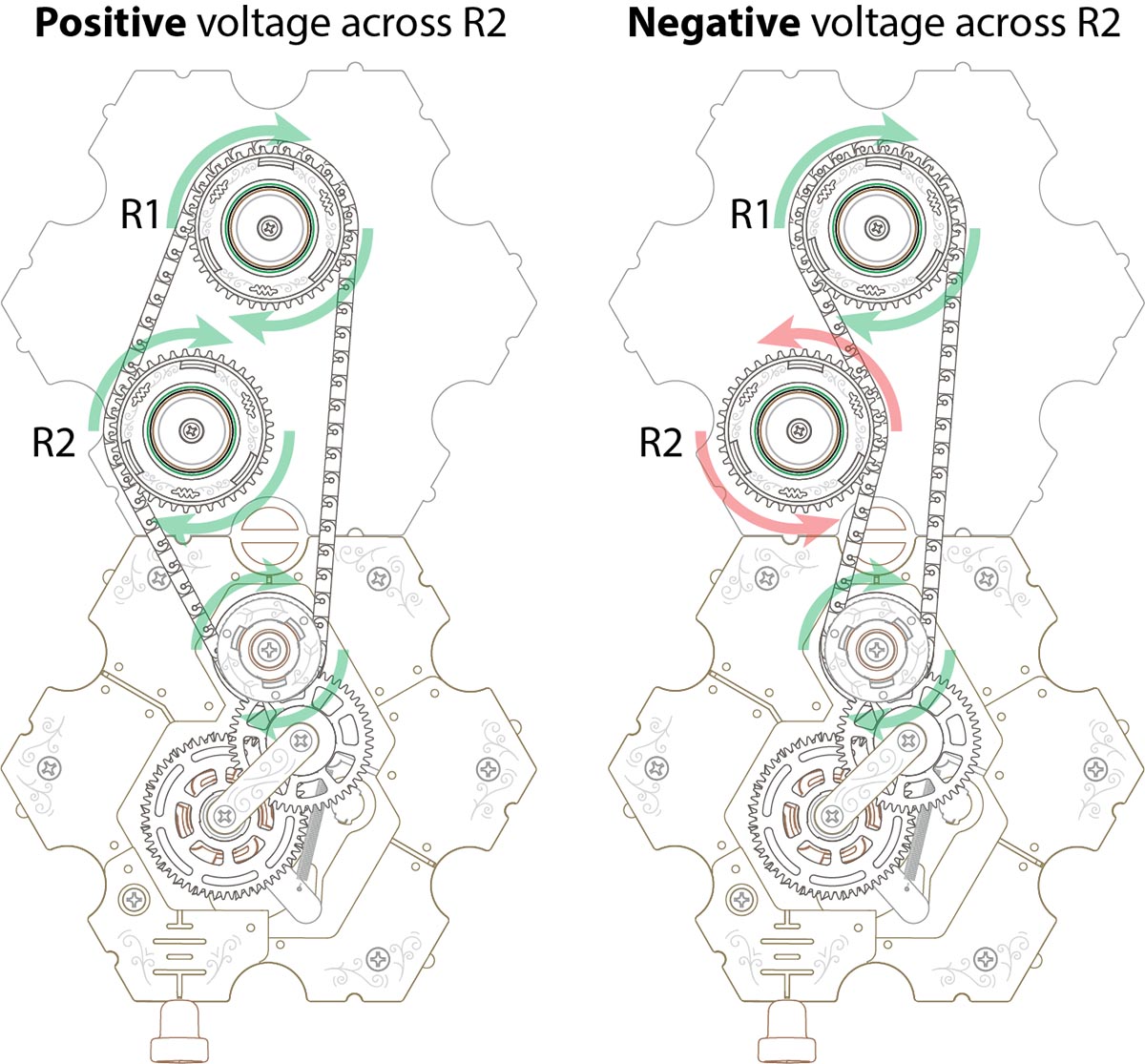
Converting positive (clockwise) to negative (counter-clockwise) voltage is as easy as putting the chain on the other side of the part.

It's also exceedingly easy to trade voltage for current or current for voltage, as a transformer does. Simply tie the top two sprockets of a junction together and it doubles or halves the voltage.

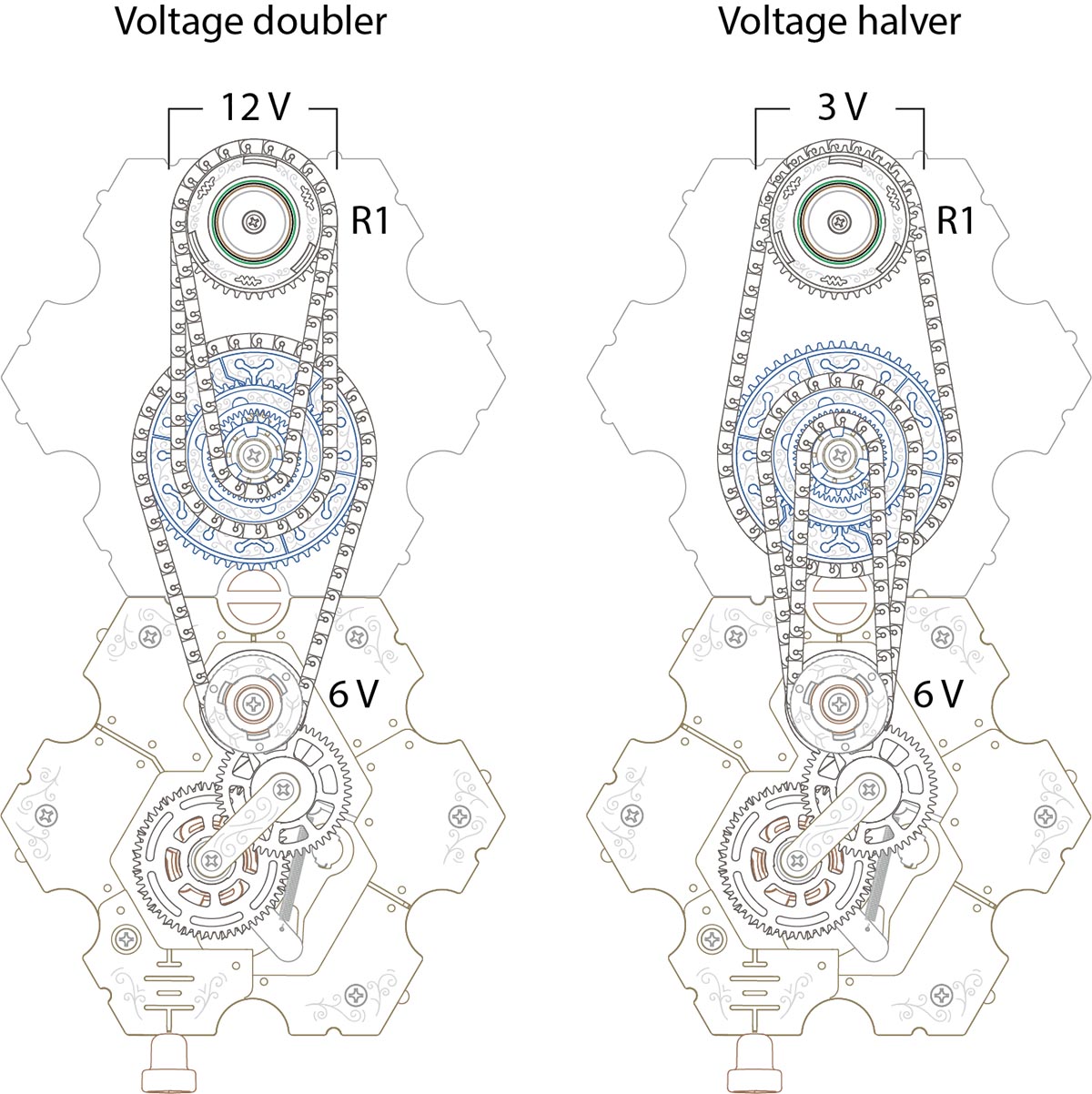
A spintronic junction can be used to easily double or halve the voltage across R1.

Spintronic transistors are also easier to use. Spintronic transistors behave like field-effect transistors (FETs) where the resistance of the source-drain depends on the voltage at the gate.

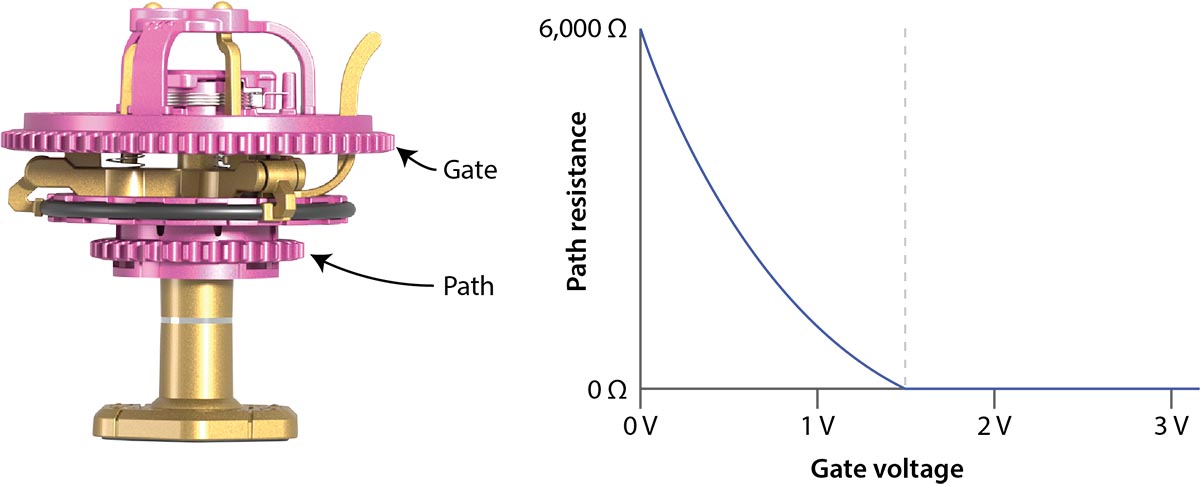
A spintronic transistor behaves like a field-effect transistor. The voltage across the gate controls the resistance of the source-drain.

But the main advantage of spintronic transistors is that the gate is isolated from the source-drain (called the "path" here). So it's simply the voltage across the gate that controls the resistance. That makes it significantly easier to design and understand transistor circuits.

Finally, let's take a look some of the math behind spintronics. Spintronics introduces the mechanical equivalent to units of voltage, current, capacitance, etc. To distinguish between the electronic and spintronic units, we add the word "spin" out front. So "volts" become "spin volts," "amps" become "spin amps," "farads" become "spin farads." Also, the abbreviations of the units have a little spinning arrow over the top:

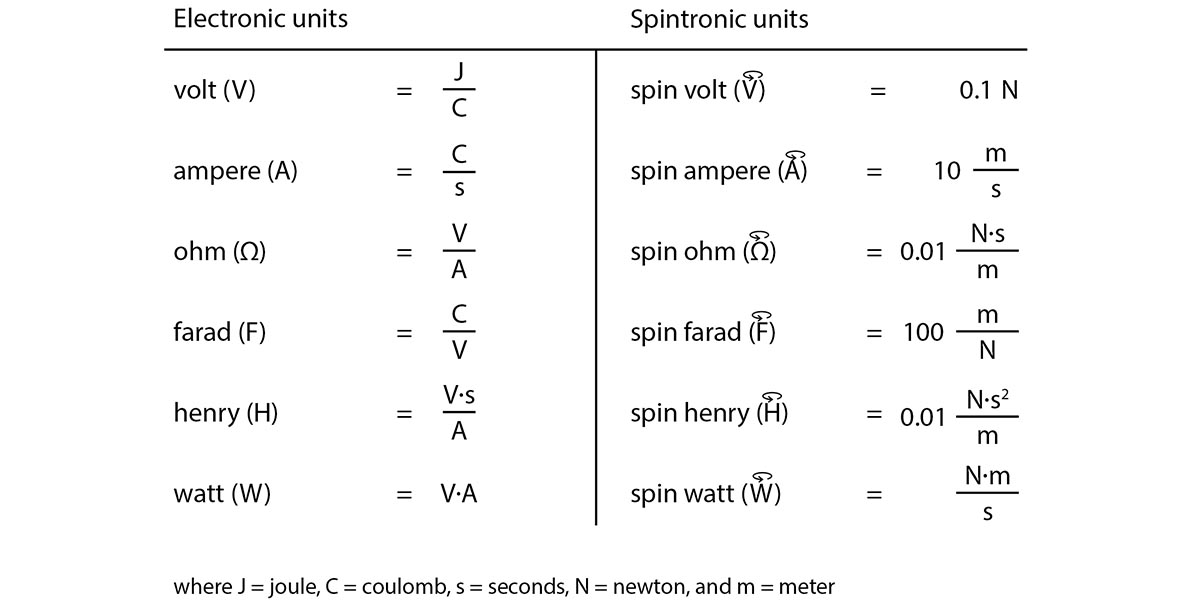
Electronic and their analogous spintronic units.

The derivation of these units comes from one key relationship that ties all of electronics to spintronics. The relationship is this:

1 spin coulomb = 10 meters of chain

What does that mean? Well, the coulomb is a unit of charge equal to 6.2415090744×10¹⁸ electrons. Therefore, in spintronics, we say that 6.2415090744×10¹⁸ electrons is the same as 10 meters of chain.

You might wonder why we picked 10 m of chain to be equal to a coulomb of charge. Why not 100 m or 1000 m of chain? Because with 10 m of chain, the values of voltage, resistance, and current all fall in the same range as those normally encountered in low voltage electronics.

Note that on most of this page, the spintronic units aren't explicitly used. They're not used here to make things less confusing, but they are used throughout the puzzle book.